15 years of sharpening a sword: Zhang Yitang proves the Riemann conjecture related problems? November paper see

Welcome to the WeChat subscription number of “Sina Technology”: techsina

Text/Aeneas so sleepy

Source/New Zhiyuan (ID: AI_era)

[Introduction to Xinzhiyuan] Recently, it was reported on the Internet that Zhang Yitang seemed to have overcome a major problem in the mathematics world. As soon as this news came out, the entire mathematics circle was shocked.

In the past two days, the rumors that Zhang Yitang “conquered” the Landau-Siegel Zeros Conjecture were overwhelming.

Zhang Yitang allegedly acknowledged this verbally while attending an online Zoom meeting of Peking University alumni on October 15.

When he solved the step from 0 to 1 of the “twin prime number conjecture”, Zhang Yitang has already caused a sensation in the mathematics circle all over the world. And if he really solves the Landau-Siegel zero-point conjecture, it will undoubtedly cause a major earthquake.

However, the related paper appears to have to wait until next month.

Let’s rub our hands and wait.

This paper was revised by Zhang Yitang for 9 years

The last time Zhang Yitang attracted so much attention on the Internet was in 2013.

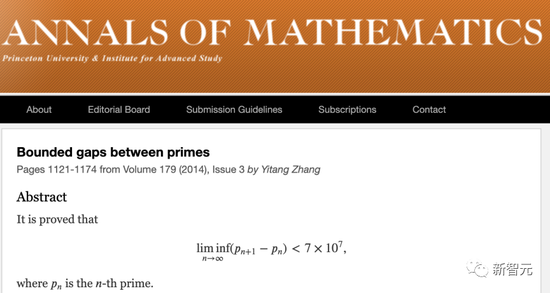
At the time, he completed the paper “Bounded Distances Between Primes”, proving “a weakened version of the twin prime conjecture”.

The paper was published in Annals of Mathematics in 2013.

As a well-known Chinese “big cow” in mathematics, most people may think that Zhang Yitang has achieved a lot.

But in fact, in his more than 40 years of academic career, he has only published a handful of papers.

Among the more famous ones, in addition to the “Weakened Twin Prime Conjecture” published in 2013, the other two were published in the “Duke Mathematics Journal” in 2001 and “Acta Mathematica” in 1985. Landau-Siegel’s zero-point conjecture.

In an interview with People Weekly, Zhang Yitang once explained: The reason for not publishing papers for a long time is because it is difficult for him to accept the “Partial result” — he already has some research that can produce results at any time, but he does not Take it out willingly, because “what you take out after it’s completely done is a big thing.”

This is different from what mainstream mathematicians do today.

Before he became famous, Zhang Yitang had studied the Landau-Siegel zero-point conjecture for many years.

In May 2007, when he was still at the University of New Hampshire, he wrote a draft of a thesis on the subject.

At that time, this paper was not complete, it was just a rough outline of the proof of the Landau-Siegel conjecture. Zhang Yitang saved it on the preprint server, then “put it down” and ran to do it. It has become the “twin prime” problem.

The prediction of the genius really makes sense. You already know what happened next.

The paper on the “twin prime number conjecture” made him explode and became the “top stream” in the academic world.

Nature featured the results in the Breaking News section. At the same time, Zhang Yitang won the heavyweight awards such as the Rove Schock Award, the Cole Number Theory Award, and the MacArthur Genius Award.

His miraculous deeds have also been reported by various media.

Now, after 9 years, because of his words, the mathematics circle is suddenly boiling again.

It should be speculated that the outline of the Landau-Siegel zero-point conjecture that he had “left behind” for many years has been supplemented, and the complete paper has been released.

This time, Zhang Yitang is preparing for the second “explosion”?

Landau-Siegel zero-point conjecture

So, what is the Landau-Siegel zero-point conjecture?

In number theory, the Landau-Siegel zero problem can be seen as a special and possibly much weaker form of the generalized Riemann conjecture.

In 2019, at the “Master Lecture” held by the Chinese University of Hong Kong, Zhang Yitang introduced the history and application of the Landau-Siegel zero-point problem, and explained why this problem is so important and difficult to solve.

According to the information compiled by the Chinese University of Hong Kong (Shenzhen), Zhang Yitang himself introduced it as follows:

What is the significance of Zhang Yitang’s research?

Why did the revelations about Zhang Yitang startle the entire math circle?

Because the Riemann conjecture is one of the most important mathematical problems in the mathematics world today, it is of great significance.

To understand its significance, we might as well understand the general background of number theory.

Number theory is a branch of pure mathematics, which studies the properties of numbers and can be said to be the purest mathematics. Famous mathematicians such as Pythagoras, Euclid, Fibonacci, Descartes, Fermat, Leibniz, Lagrange, Euler, Gauss, Hilbert, etc. It left an indelible mark in the history of research.

The study of number theory has produced many conjectures, which will greatly promote the progress of mathematics.

In 1900, German mathematician David Hilbert put forward “23 mathematical problems that mathematicians should strive to solve in the 20th century” at the Second Congress of Mathematicians.

In 2000, the “Millennium Prize Problem” of the Cray Institute of Mathematics put forward seven important conjectures. If this conjecture can be solved, amazing breakthroughs will occur in the fields of cryptography, aerospace and communication.

Among the many conjectures, the Riemann conjecture is the only conjecture that appears in both Hilbert’s 23 problems and the Millennium Prize problem.

Although Riemann’s conjecture is not as well known as Fermat’s conjecture and Goldbach’s conjecture, its mathematical importance is far greater than the latter two. The Riemann conjecture and Fermat’s last theorem have become the geometric topology carriers of m-theory fused with general relativity and quantum mechanics.

At present, many conjectures of number theory have been confirmed. In 1995, Fermat’s last theorem was proved; in 2002, the Catalan conjecture was proved; in 2013, the twin number conjecture was proved; in 2013, the odd Goldbach problem was proved.

But the Riemann conjecture has remained unsolved. It is conceivable that if someone proves the Riemann conjecture, it will be a sensational event.

In the same way, if the Riemann conjecture is falsified, it is also an earth-shattering event in the mathematics community.

And if Zhang Yitang really falsifies the Riemann conjecture, or proves the existence of Landau-Siegel zero, it will undoubtedly be nuclear explosion-level news.

Riemann conjecture

Let’s look at the origin of the Riemann conjecture.

In 1859, the German mathematician Riemann first mentioned this conjecture in his paper “On the Number of Prime Numbers Less Than a Given Value”.

In this regard, “Science Big Shake House” happened to give a very vernacular explanation to this in an article.

We all know that the numbers 2, 3, 5, 7, and 11, except 1 and itself, cannot be divisible by other positive integers, so they are called prime numbers. All positive integers greater than 1 can be represented by the product of prime numbers.

But if you want to ask: “How many prime numbers are smaller than a certain number? What is the distribution of prime numbers in the whole sequence?”

This problem is complicated.

Riemann found that the distribution of prime numbers is closely related to a function:

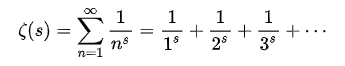
In this formula, s is a complex number, which can be written in the form s=a+bi (a is the real part of s, b is the imaginary part of s, and i is the radical minus one).

Mathematicians can easily prove that as long as the real part of s is greater than 1, then in the entire infinite series, after adding the absolute value of each term, a result that converges and approaches a certain fixed value will be obtained.

However, for the case where the real part of s is less than 1, things are not so simple: the whole series sum may diverge.

But we also want to expand the definition of the function to make it applicable to a wider range, so what should we do?

With some “simple” mathematical tricks, the Riemann zeta function above can be rewritten as:

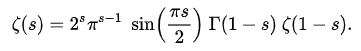
Among them, Г is called the gamma function.

It can be found that when s is a negative even number (s= -2, -4, -6…), the Riemann zeta function is zero. These values ​​of s are called trivial zeros.

However, in addition to the trivial zeros, there are other values ​​of s that can make the Riemann zeta function zero—called non-trivial zeros; not only do they have a decisive influence on the distribution of prime numbers, but the real parts are all located between zero and one between.

At this point, it has reached the difficulty that Riemann himself cannot prove.

However, he made a guess that these non-trivial zeros have a common property: the real part of all non-trivial zeros of the Riemann zeta function is one-half.

This is the famous Riemann conjecture.

Twin prime conjecture

Finally, let’s take a look at the papers related to the “twin prime number conjecture” that made Zhang Yitang famous.

After graduating from Purdue University with a Ph.D. in 1992, Yitang Zhang had a rough time. Finally, in 2013, his proof of “there are infinitely many pairs of prime numbers with a difference of less than 70 million” was accepted by the Annals of Mathematics within five weeks. .

In this paper, he found the upper bound of the difference between twin prime pairs – 70 million, which is a major progress in the “twin prime conjecture”, achieving a leap from 0 to 1.

Later, Tao Zhexuan and other mathematicians quickly narrowed the gap to 246, but this is equivalent to a leap from 1 to 2. In comparison, Zhang Yitang’s step from 0 to 1 is more significant.

The research results of the two mathematicians have been made into a documentary.

According to “Guangming Daily” reporter Wang Qinghuan, at the “Seeking Truth Award Ceremony” in 2016, the famous scientist Yang Zhenning once explained Zhang Yitang’s research in a language that elementary school students can understand——

Regarding the above explanation, Zhang Yitang himself said: “Professor Yang Zhenning’s introduction is both popular and clear. If I had to explain it myself, I would definitely not be able to explain it so well.”

At present, there has been heated discussion in the community, if the legend is true, whether Zhang Yitang’s achievements can surpass Qiu Chengtong and Chen Jingrun.

Let’s wait for November to see if Zhang Yitang will hand over a “big thing” to his satisfaction.

(Disclaimer: This article only represents the author’s point of view and does not represent the position of Sina.com.)

This article is reproduced from: http://finance.sina.com.cn/tech/csj/2022-10-17/doc-imqqsmrp2846214.shtml
This site is for inclusion only, and the copyright belongs to the original author.