Implementing quantum convolutional neural networks on superconducting quantum processors for quantum phase identification

the public/ ScienceAI (ID: Philosophyai)

Edit | Radish Skin

Quantum computing critically relies on the ability to efficiently characterize the quantum states output by quantum hardware. Traditional methods of probing these states through direct measurements and classically computed correlations become computationally expensive when increasing system size. Quantum neural networks that identify specific features of quantum states by combining unitary operators, measurements, and feedforward promise to require fewer measurements and tolerate errors.

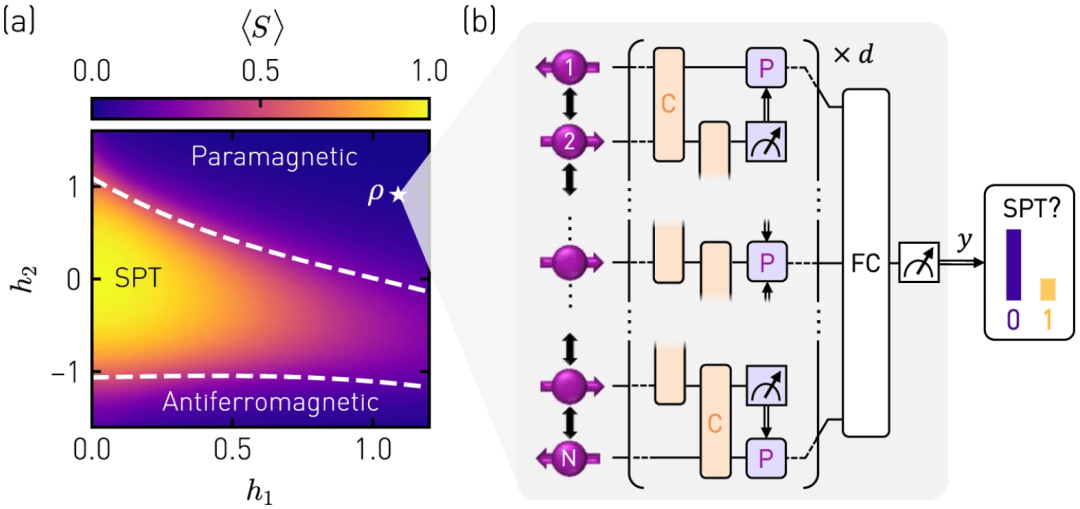
Here, a research team from ETH Zurich implemented a quantum convolutional neural network (QCNN) on a 7-qubit superconducting quantum processor to identify symmetry-protected topologies of spin models characterized by non-zero string-order parameters ( SPT) phase.

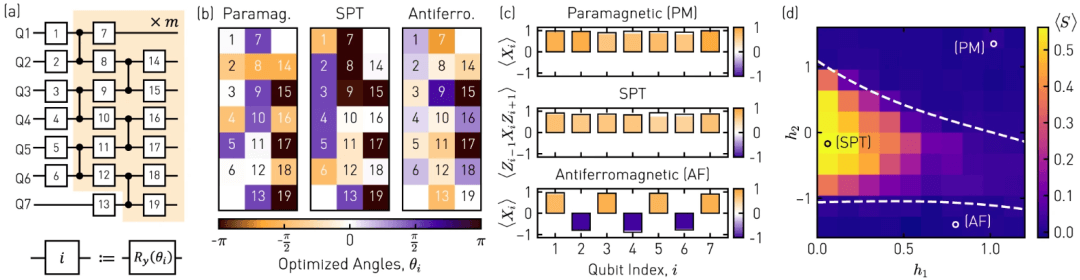
The researchers benchmark the performance of QCNNs based on a set of approximate ground states of the cluster Ising Hamiltonian, which they prepare using hardware-efficient low-depth state preparation circuitry. Although the QCNN itself consists of finite-fidelity gates, it identifies topological phase with a higher fidelity than directly measuring the chord-order parameter of readiness.

The study, titled “Realizing quantum convolutional neural networks on a superconducting quantum processor to recognize quantum phases”, was published in Nature Communications on July 16, 2022.

Remarkable progress in building quantum hardware has propelled the exploration of potential near- and future applications of error-correcting quantum computers, especially in the simulation and machine learning of quantum many-body systems. For example, the ability of quantum computers to perform linear algebra operations more efficiently could provide potential speedups for classical machine learning tasks, such as ordinary matrix inversion in linear regression models.

However, dedicated quantum algorithms for this purpose, such as Harrow, Hassidim, and Lloyd’s algorithms, rely on both executing deep quantum circuits and loading binary data into quantum registers to provide practical advantages, which are currently available on quantum hardware impossible.

In order to load classical data into quantum registers in a more resource-efficient way and map their features to high-dimensional Hilbert spaces for easy classification, a team designed quantum circuits parameterized by input data and used them for quantum Support Vector Machines and Quantum Neural Networks. However, independent of specific data embedding schemes, it remains an open question whether tasks aimed at analyzing classical data can fully exploit the ability of quantum computers to handle data volumes that cannot be represented classically.

Therefore, promising algorithms to exploit the capabilities of near-term quantum computers are those that process quantum data directly and do not have classical simulations. Quantum computers are beginning to reach a level where their output states are too complex to be analyzed by classical means, suggesting that machine learning techniques that directly process quantum data promise to be an increasingly important tool for effectively characterizing and benchmarking quantum hardware. Examples of its specific applications include principal component analysis of density matrices, quantum autoencoders, proof of Hamiltonian dynamics, and detection of entangled correlations in quantum many-body states.

Graphic: The concept of the quantum phase recognition experiment. (Source: Paper)

In a newly published study, researchers at ETH Zurich have experimentally demonstrated the classification of quantum states through quantum neural networks by implementing a quantum algorithm aimed at identifying the signature of topological quantum phases. This challenging task has important implications for studying quantum many-body systems such as high-temperature superconductors. Previous work in this area has focused on identifying topological quantum phases from (simulated) measurement data using classical machine learning techniques.

Furthermore, topological states have recently been prepared on quantum hardware and analyzed by measuring characteristic observables such as string order parameters.

Illustration: Variational ground state preparation. (Source: Paper)

Here, the researchers experimentally demonstrate a new paradigm to detect symmetry preservation on 7-qubit quantum devices by preparing quantum states in and out of the SPT phase and further processing these states through a quantum convolutional neural network to perform quantum phase identification Topological state. They designed and experimentally implemented a QCNN that, despite itself consisting of finite-fidelity gates, outperformed direct measurement of string-order parameters in correctly identifying topological phase.

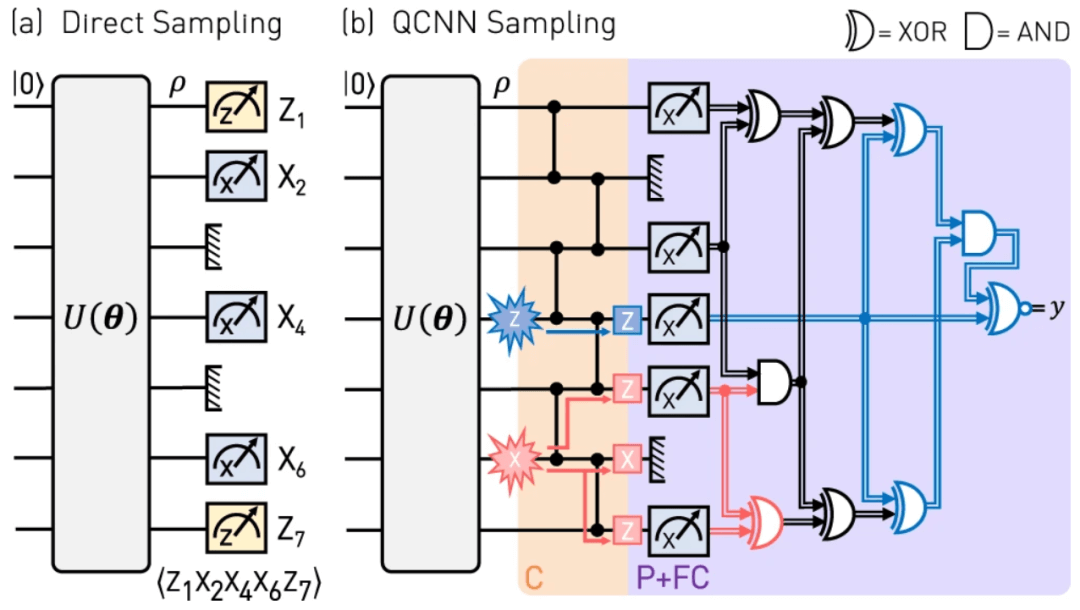
Pictured: Quantum phase recognition circuit. (Source: Paper)

This enhanced capability is achieved by building a QCNN to simultaneously measure the weighted sum of Pauli strings, the number of which grows exponentially with the system size N. The structure of this efficient measurement observable allows the QCNN to tolerate both X- and Z-type errors when dealing with weakly perturbed input states. Using a QCNN to measure this observable avoids the need to measure its components individually.

Graphic: QCNN performance. (Source: Paper)

By implementing QCNN on a superconducting quantum processor, the researchers demonstrated its ability to efficiently identify quantum phases. With further advances in the number of qubits and circuit depth, QCNNs are expected to become important diagnostic tools for characterizing the output state of NISQ devices, which are increasingly challenging to analyze using classical computing.

Such applications would benefit from the expected increased sampling complexity at phase boundaries; here, QCNNs enhance the discriminative ability to assign states to different quantum phases. While this enhancement is not yet available for the system sizes considered here, larger systems will be able to benefit from it.

Furthermore, the scaling advantage can be understood by representing the output of the QCNN as an equivalent weighted sum of string order parameters, the number of which grows exponentially with N. Therefore, QCNN allows one to measure the sum of all these terms simultaneously. An interesting direction to be explored in future work involves the trainability of parameterized QCNNs.

Paper link: https://ift.tt/79Hfi6u