
Welcome to the WeChat subscription number of “Sina Technology”: techsina
Text/Jin Lei Alex
source/qubit
Breaking News!
The online mathematician Zhang Yitang has conquered the Landau-Siegel Zeros Conjecture.
And this news is said to be said by Zhang Yitang himself when he participated in the Zoom online meeting of Peking University alumni.
Such a revelation can be described as a sensation in the mathematics community.
Weibo blogger “Physical Cheese Mathematical Sauce” believes that if what Zhang Yitang proves is the existence of Landau-Siegel zero, then the Riemann conjecture can die:
Zhang Yitang is directly the greatest mathematician in the past 50 years, no one.
But at the same time, he believes that “this is too appalling”, so he is more inclined to think that what Zhang Yitang has proved is that Landau-Siegel zero does not exist – “this is also a more convincing conclusion”.
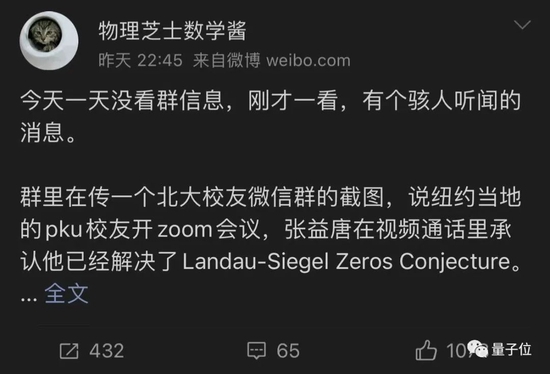
But the value of this work can be said to be beyond doubt, as Zhihu netizens broke the news:
If Zhang Yitang can make Landau-Siegel, it is equivalent to being struck by lightning twice.
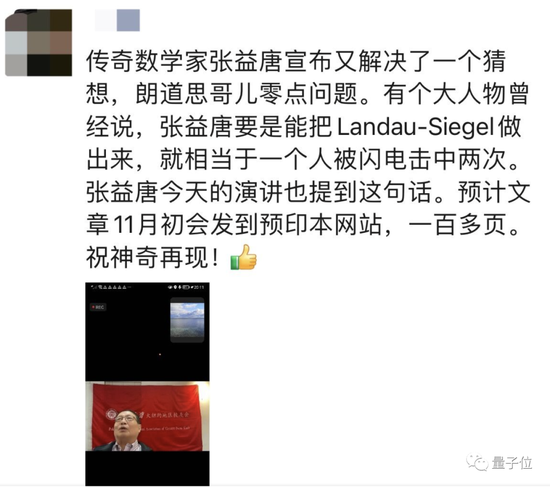
And according to this breaking news, the relevant article will be sent to the preprint website in early November, with more than 100 pages.
So what exactly is this Landau-Siegel zero-point conjecture?
Why does the proof of it cause such a repercussion?
Landau-Siegel zero-point conjecture
The so-called Landau-Siegel zero-point conjecture is simply a weak form of the Riemann conjecture.
A central question to answer is whether there is such a thing as a Landau-Siegel zero.
First we set real numbers σ, t and complex numbers s=σ+it.
According to the introduction of Zhihu blogger “TravorLZH”, mathematicians in the 19th century introduced the Riemann conjecture in order to study the distribution of prime numbers.
In order to study the distribution of prime numbers on arithmetic sequences, mathematician Dirichlet introduced the L function.
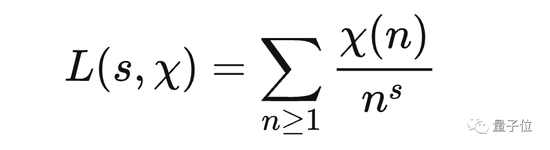
Later, mathematicians also developed corresponding analytical tools to explain that the L function has no zeros when σ=1, thus proving the prime number theorem on arithmetic progressions:
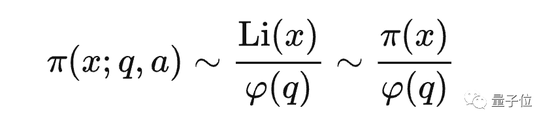
However, mathematicians are still dissatisfied with the above formula, and they will continue to reduce the existence area of non-trivial zeros of the L function.
So predecessors have proved that the non-trivial zeros of the L function can basically fall in an hourglass-shaped region similar to the following formula:
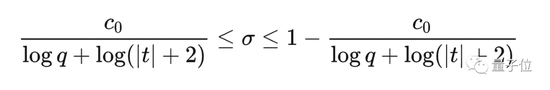
If all non-trivial zeros of the L function fall within this region, the arithmetic sequence prime number theorem with remainder can be obtained.
Unfortunately, mathematician Edmund Landau found that when X satisfies special properties, its corresponding L function may have an exceptional zero that falls outside the above formula.
But luckily, Landau proved that for every such L-function, if there is an anomalous zero in the region below, only one such zero is possible, and the order is exactly one.
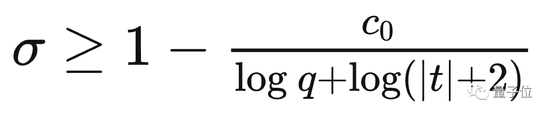
Later Walfisz used this weaker non-zero region to obtain a compromised version of the arithmetic prime number theorem:
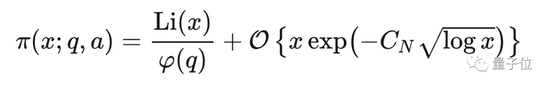
Obviously, this formula has many more restrictions, so of course we hope that the L function can have no abnormal zeros.
Because of the pioneering work done by two mathematicians, Landau and Siegel, in the field of L-function anomalous zeros, the anomalous zeros are often referred to as Landau-Siegel zeros.
The conjecture that asserts that the L function has no anomalous zeros is called the Landau-Siegel conjecture.
Overall, the generalized Riemann conjecture is just a sufficient condition for the Landau-Siegel conjecture.
But this century of research has shown that the Landau-Siegel problem can be harder to solve than the Riemann conjecture.
Therefore, if Zhang Yitang proves the Landau-Siegel zero, then the Riemann conjecture is wrong.
That’s why everyone described the news as “appalling”.
But for now, many people are more inclined to think that what he has proved is that the Landau-Siegel zero does not exist.
In this way, there will be no conflict with the Riemann conjecture.
As for the specific proof, we still need to wait for a positive reply from Zhang Yitang himself.
And many netizens think about it:
Considering Zhang’s life, he is calm and determined, and he will definitely not talk nonsense.
However, it should be noted that so far, Zhang Yitang himself has not announced this progress on other occasions and forms.
Dormant for half a lifetime, a blockbuster
In fact, regarding the Landau-Siegel conjecture, Lao Zhang pre-printed a paper as early as 2007, but the argument in it was somewhat buggy.
He has since mentioned several times that he is following the issue.
Then in 2019, Zhang said that some gratifying progress had been made on this conjecture.
But to say that Zhang Yitang has grown from obscurity to fame, we have to set the time pointer to 2013.
That year, he published “Bounded Intervals Between Prime Numbers” in the Annals of Mathematics, the highest journal of mathematics.

This article proves for the first time that there are infinite pairs of prime numbers with limited distances, and has made a qualitative breakthrough in the number theory problem of the twin prime number conjecture.
Before this paper was published, he had an enviable experience of studying in top Chinese and foreign universities, but then he went through years of dormancy, and even had to go to Subway to serve dishes.
From 1978 to 1985, Zhang Yitang received his undergraduate and master’s degrees from Peking University’s School of Mathematics, and studied under the famous Chinese mathematician Pan Chengbiao during his master’s degree.
Later, algebraic geometer Mo Zongjian visited Peking University and excavated Zhang. Zhang then followed Mo to the United States to pursue a Ph.D. at Purdue University (the so-called “cradle of astronauts”).
When Zhang finally submitted his doctoral dissertation, he had been at Purdue University for six and a half years, but during that time he had published few academic papers.
It is worth mentioning that Zhang Yitang himself did not like algebraic geometry very much, but was more keen on number theory.
So he hoped to leave this circle after graduating from the Ph.D. and go back to study the number theory that he was interested in, but his tutor Mo Zongjian was not happy when he learned about it, so the two became more and more divided.
As a result, when Zhang finally graduated with a Ph.D., he did not have a job recommendation letter from his supervisor.
(Mo Zongjian once clarified the matter after Zhang Yitang became famous, thinking that he did not write a recommendation letter because he did not know whether it was appropriate to recommend a ready-made job to Zhang, and said that this practice was not very popular at that time)
Coupled with his introverted personality and too few academic papers published during his Ph.D., no American university or research institute is willing to ask him.
A friend once suggested to Zhang to change careers in finance or computer industry, but he was not willing.
On the one hand, he continued to study number theory; on the other hand, he also had to make a living, but unfortunately for a long time, he could not find a good job, and sometimes he even had to live in the basement of a friend’s house.
During this period, he worked as an accountant at Subway, a fast-food chain run by a Peking University alumnus. Because it allows him to use his memory and calculation skills at work, and to take time out to study mathematics.
Fortunately, another “Bole” in his life appeared, it was Tang Puqi, his alumnus at Peking University and Purdue University.
In 1999, Zhang Yitang and Tang Puqi jointly published an Internet patent. The patent involved a very practical computer algorithm problem, but Zhang solved it in just three weeks, which made Tang impressed.
Therefore, Tang Puqi introduced Zhang Yitang to Ge Liming, who taught at the University of New Hampshire, and then recommended by Ge Liming, Zhang Yitang served as a teaching assistant and lecturer in the Department of Mathematics and the Department of Statistics, teaching calculus, algebra, elementary number theory and other courses.
At this point, he finally returned to the academic circle, and has a convenient channel to follow new progress, understand the thoughts of his peers, and download academic papers.
…
As for the Landau-Siegel zero-point conjecture about this exposure, we will continue to pay attention.
Reference link:
[1]https://mp.weixin.qq.com/s/QSmHDBGYwGy-mCMjVj-GDw[2]https://https://ift.tt/xLEhVcY
[3] https://https://ift.tt/m0TwRZJ
[4] https://https://ift.tt/7z0d6Aq
[5] https://ift.tt/jKLFriJ type=comment

(Disclaimer: This article only represents the author’s point of view and does not represent the position of Sina.com.)
This article is reproduced from: http://finance.sina.com.cn/tech/csj/2022-10-16/doc-imqmmthc1068528.shtml
This site is for inclusion only, and the copyright belongs to the original author.