Luogu P6295. Labeled DAG count

Original link: https://www.shuizilong.com/house/archives/luogu-p6295-%E6%9C%89%E6%A0%87%E5%8F%B7-dag-%E8%AE%A1%E6 %95%B0/

For labeled graphs, assuming that we have obtained the EGF in the case of disconnection, then there are common routines for finding the corresponding connected graph (see the problem of urban planning and the problem of desert ).

Therefore, the problem is converted into a disconnected situation, which is the previous problem .

We need to find a way to construct the convolution first.

(1) $\begin{align*} f_i &= \sum_{j=1}^{i} (-1)^{j-1} \binom{i}{j} \sum_{k=1}^{i-j} f_{i-j} 2^{j(i-j)} \end{align*}$

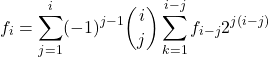
Here you need to use some tricks, and finally get it.

(2) $\begin{align*} F(x) &= \sum_{i} x^i \frac{f_i}{i!2^\binom{i}{2}} \\ G(x) &= \sum_{i} x^i \frac{(-1)^{i+1}}{i!2^\binom{i}{2}} \end{align*}$

 
  
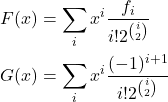
#include <lastweapon/poly> 
  
#include <lastweapon/number> 
  
using namespace lastweapon; 
  
 
  
const int N = int(1e2) + 9; 
  
 
  
LL C2(LL n) { 
  
    return n*(n-1)/2; 
  
} 
  
 
  
int main() { 
  
#ifndef ONLINE_JUDGE 
  
    //freopen("in.txt", "r", stdin); 
  
#endif 
  
    int n; RD(n)++; 
  
 
  
    Poly F(n); Mint i2 = invFac[2]; 
  
 
  
    FOR(i, 1, n) { 
  
        F[i] = invFac[i] * pow(i2, C2(i)); 
  
        if (i&1) F[i] = -F[i]; 
  
    } 
  
 
  
    F[0] += 1; F = F.inv(n); 
  
    REP_1(i, n) F[i] *= pow(Mint(2), C2(i)); 
  
    F = F.log(n); 
  
 
  
    --n; 
  
    REP_1(i, n) { 
  
        cout << F[i] * fac[i] << endl; 
  
    } 
  
}

This article is reproduced from: https://www.shuizilong.com/house/archives/luogu-p6295-%E6%9C%89%E6%A0%87%E5%8F%B7-dag-%E8%AE%A1%E6 %95%B0/
This site is only for collection, and the copyright belongs to the original author.