Original link: https://editor.leonh.space/2023/or-tools/
The OptaPy and OptaPlanner solvers were introduced earlier. This article is about another solver OR-Tools produced by Google. For the integrity of the article, before entering OR-Tools, let’s quickly introduce what is a planning problem. and what is a solver.
Planning problems and solvers
For general users, they can create some formulas and goals in spreadsheets such as LibreOffice Calc, and then use the solver function to help them find the cell combination that is closest to the goal, such as “How to give change so that customers will not be disappointed?” Got a lot of coins?” In the model of the solver, we changed the question into this form: “How to combine banknotes and coins of various denominations so that the customer gets the least amount of currency and the amount is Right?” Let’s represent this question in the following diagram:
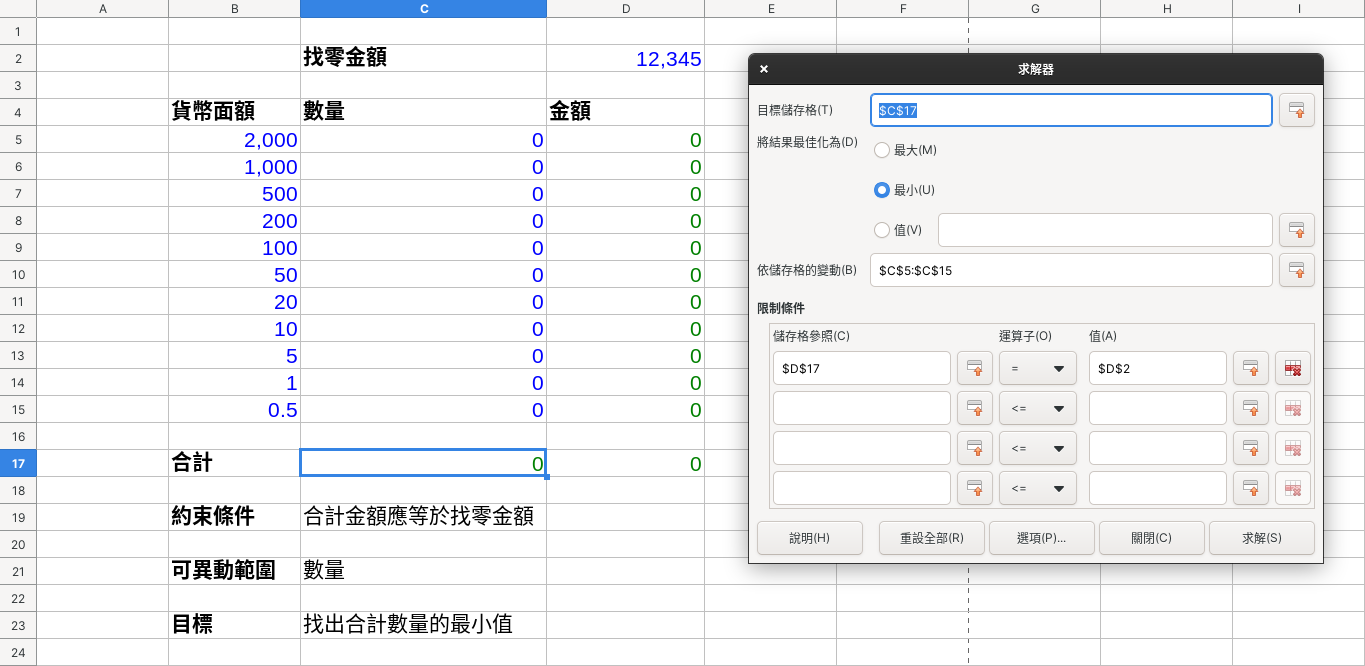
The final solution is as follows:
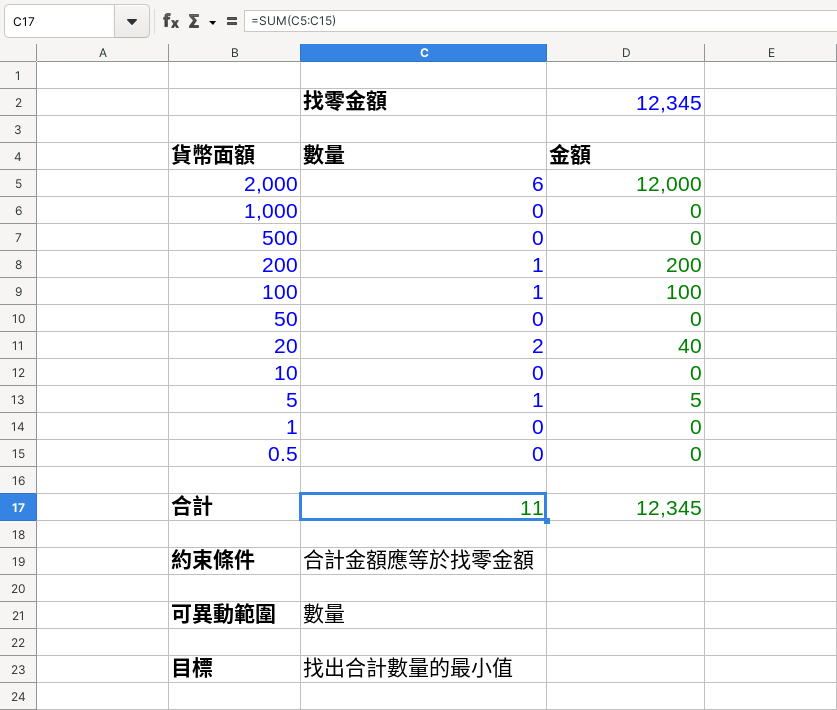
In the end, the customer gets 11 various currencies, and the amount is correct (see ” Knowledge Solver ” for details).
Problems like the above are linear programming problems, but there are more complex problems, such as:
- Scheduling, scheduling, and job scheduling, how can scheduling be fair and meet the needs of multiple parties?
- The route planning problem, how to go to maximize the transportation efficiency?
- Packing problem, how to pack to maximize the utilization of the box?
- Cutting problem, how to cut to maximize material utilization?
- The problem of the competition, how to arrange the competition to make the competition fair and not strong?
- Investment problem, how to configure to maximize the return?
The common feature of these problems is “complicated calculation and simple verification”. The reason why the calculation is complicated is that there are nearly infinite possibilities . There are infinite possibilities, and the reason why the verification is simple is that if you have really traveled all over Taiwan, you can verify it in seconds with the coordinates.
For this type of problem, it is impossible for us to exhaust all the possibilities and find the best solution, because the time spent in this way may be astronomical, but we can use the solver to help us find the “approximate best solution”, In the case where the theoretical “true optimal solution” cannot be obtained, the approximate optimal solution is sufficient to meet our needs.
OR-Tools
OR-Tools is a solver developed by Google. The “OR” in the name means operations research, which is a discipline that scientifically discusses various operational problems. OR-Tools itself is developed in C++ and provides APIs in multiple languages. Since C++ can be directly compiled into the native binary files of each platform, it does not have to wait for the JVM to run like OptaPy. Even in the world-renowned OR-Tools The slow language Python can solve problems in seconds, which not only improves efficiency, but also reduces customer complaints.
There are multiple solvers in OR-Tools. Each solver is a set of algorithms. They have their own strengths. Some are suitable for solving linear problems, and some are suitable for solving constrained problems. Because my needs are constrained problems, So the following will only talk about the constraint problem solver CP-SAT in OR-Tools.
Installing OR-Tools in Python is just that eternal pip install :
$ pip install ortools
CP-SAT by OR-Tools
CP-SAT is one of the built-in solvers of OR-Tools, “CP” means constraint programming (constraint programming) , “SAT” means Boolean satisfiability problem (Boolean satisfiability problem) , these technical terms are a bit difficult, simply put It is the planning problems mentioned above, and CP-SAT is a solver for such problems.
There are several major steps in using OR-Tools:
- create variable
- make constraints
- set a goal
- execute solve
No matter which solver is used, most of these steps are the same, including the solver in LibreOffice Calc, OptaPy, and OptaPlanner. The difference lies in the different thinking modes for building problem models. On the side of OR-Tools, we need to put the specific Problems are expressed in the form of mathematical equations. Although they are mathematical equations, they are actually in the form of codes. That is to say, the thinking mode in our brains must go through the three stages of “understanding the problem→mathematicalization→programming” when modeling. stage, this process does not require us to be mathematics experts, but it requires strong logical thinking, which is also the gap that is difficult for people with weak logic to bridge.
Anyway, the head is out of the way, so let’s get on with it.
simple constraint problem
A simple constraint problem is as follows:
- There are three variables x, y, z, and their values can be 0, 1, 2.
- x is not equal to y.
- What is the largest possible x + y + z?
Create a cp_example.py script, first introduce the suite, and create a CpModel instance, named model :
"""Simple solve""" from ortools.sat.python import cp_model
"""Minimal CP-SAT example to showcase calling the solver""" # Create solver model model = cp_model. CpModel ()
Later we will use a series of model methods to build problem models.
Then create three variables x, y, z, all of which are integers ranging from 0 to 2.
Use NewIntVar() method to create integer variables, where lb and ub represent the lower bound and upper bound respectively. As for the specific values of x, y and z, it is not yet determined and will not be known until the final execution of the solution.
# Create the variable. x = model. NewIntVar ( lb = 0 , ub = 2 , name =' x ') y = model. NewIntVar ( lb = 0 , ub = 2 , name =' y ') z = model. NewIntVar ( lb = 0 , ub = 2 , name =' z ')
Then create a constraint, here the constraint is “x is not equal to y”:
# Create the constraints model. Add ( x != y )
Then set the goal, the goal is that the combination of the three should be as large as possible:
# Objective model. Maximize ( x + y + z )
In the above two paragraphs of parameters similar to mathematical formulas, it is easier to read by adding spaces between operators and operands as in general formulas, especially when the formulas become complicated.
Then you can perform the solution:
# Create a solver and solve the model solver = cp_model. CpSolver () status = solver. Solve ( model =model)
The status is just a string indicating the status of solving the problem. If the content is OPTIMAL or FEASIBLE , it means that a solution has been found. In addition to whether there is a solution, we are also very concerned about the final value of x, y, z and the combination of the three.
To obtain the value of the model variable, use Value() method of solver . To obtain the target value, which is the combination of the three, use ObjectiveValue() method of solver . The example is as follows:
if status == cp_model. OPTIMAL or status == cp_model. FEASIBLE : print ( f ' Maximum of objective function: {solver. ObjectiveValue ()} \n ') print ( f ' x = {solver. Value ( expression =x)}') print ( f ' y = {solver. Value ( expression =y)}') print ( f ' z = {solver. Value ( expression =z)}') else : print (' No solution found. ')
The output is as follows:
Maximum of objective function: 5.0
x = 1 y = 2 z = 2
In addition, there are some statistical indicators when solving:
# Statistics. print (solver. ResponseStats ())
The output is as follows:
CpSolverResponse summary: status: OPTIMAL objective: 5 best_bound: 5 integers: 1 booleans: 0 conflicts: 0 branches: 0 propagations: 0 integer_propagations: 1 restarts: 0 lp_iterations: 0 walltime: 0.00235364 usertime: 0.00235602 deterministic_time: 0 gap_integral: 0 solution_fingerprint: 0xbc76f3d3e780d9b7
The final complete code is as follows:
"""Simple solve""" from ortools.sat.python import cp_model
"""Minimal CP-SAT example to showcase calling the solver""" # Create solver model model = cp_model. CpModel ()
# Create the variable. x = model. NewIntVar ( lb = 0 , ub = 2 , name =' x ') y = model. NewIntVar ( lb = 0 , ub = 2 , name =' y ') z = model. NewIntVar ( lb = 0 , ub = 2 , name =' z ')
# Create the constraints model. Add ( x != y )
# Objective model. Maximize ( x + y + z )
# Create a solver and solve the model solver = cp_model. CpSolver () status = solver. Solve ( model =model)
if status == cp_model. OPTIMAL or status == cp_model. FEASIBLE : print ( f ' Maximum of objective function: {solver. ObjectiveValue ()} \n ') print ( f ' x = {solver. Value ( expression =x)}') print ( f ' y = {solver. Value ( expression =y)}') print ( f ' z = {solver. Value ( expression =z)}') else : print (' No solution found. ')
# Statistics. print (solver. ResponseStats ())
The above example is much simpler than OptaPy, especially suitable for fool developers like me, and don’t doubt the ability of OR-Tools just because it looks simple. After using OptaPy and OR-Tools initially, I personally My experience is that before doubting whether they can be done, you should first ask yourself whether you have correctly understood the problem, and whether you can establish a relative problem model from the problem.
This article briefly introduces Google’s OR-Tools solver, as well as some of the most basic knowledge, and I will write more in-depth parts after I understand it. :p
This article is transferred from: https://editor.leonh.space/2023/or-tools/
This site is only for collection, and the copyright belongs to the original author.