Original link: https://www.kingname.info/2022/06/22/bisect-left/
I believe everyone knows binary search. In an ordered list, using binary search can quickly determine whether the target is in the list with O(logN) time complexity.
The code for binary search is very simple, and it only takes a few lines of code to use recursion:
1 |
def binary_search (sorted_list, target) : |
The operation effect is shown in the following figure:
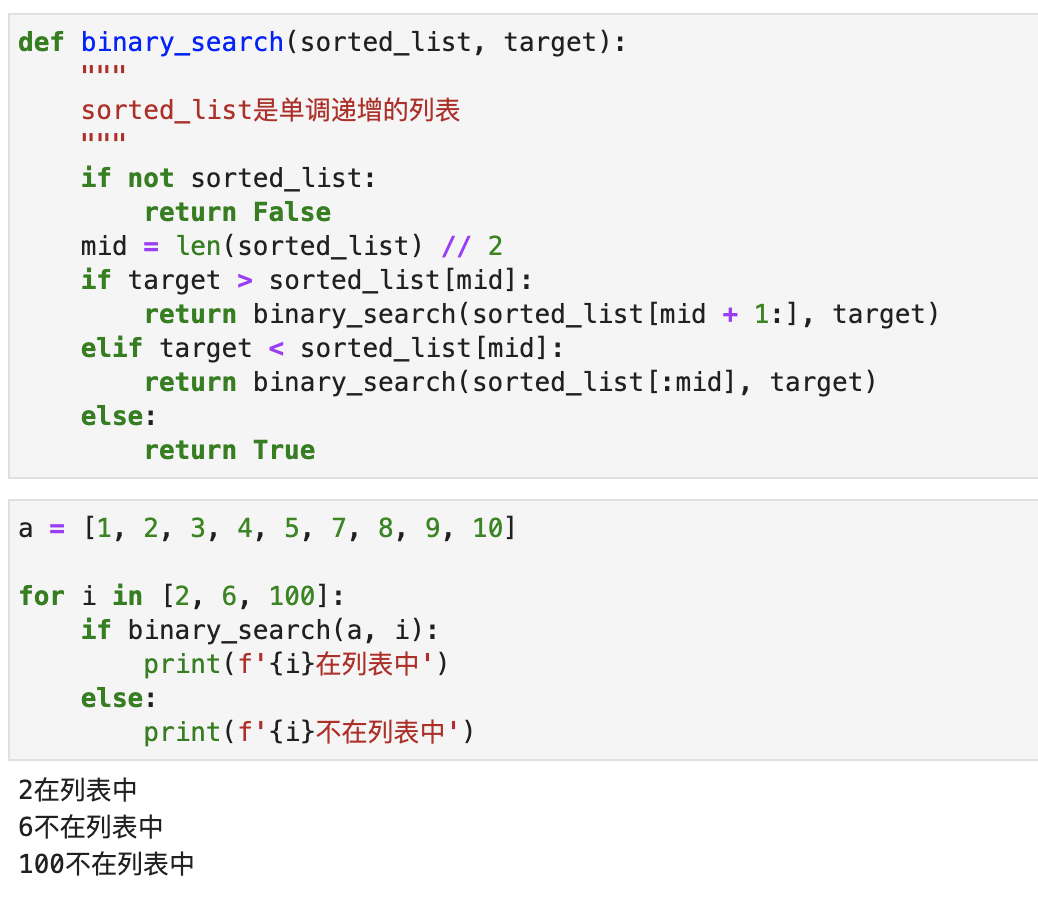
Python comes with a binary search module called bisect , which can also implement binary search, but its execution result is a bit different from the effect of our code above:
1 |
import bisect |
The operation effect is shown in the following figure:

As you can see, bisect.bisect() returns an index. If the number to be searched is already in the list, then it returns the index of最右边target number in the list + 1. Taking the list [41, 46, 67, 74, 75, 76, 80, 86, 92, 100] for example, to search for 75 . Since the index of 75 in the original list is 4 . So return the索引+1 which is 5. If 75 appears many times in the original list, such as [41, 46, 67, 74, 75, 75, 76, 80, 86, 92, 100] then最右边is returned That 75 corresponds to the index +1 , which is 6 .
If the number you are looking for is not in the original list, then bisect.bisect() will return an index. When we insert the target number into the list at the corresponding index position, the list is still in order. For example [41, 46, 67, 74, 75, 76, 80, 86, 92, 100] , we look for 82 . It returns 7 . The position of index 7 in the original list is the number 86 We insert 82 into this position, and the original data is shifted one place backward in turn. At this time, the list is still in order.
The bisect module also has a function called bisect.bisect_left() . If the target number is in the original list, then the index corresponding to the leftmost number is returned. If it is not in the list, the returned index is still in order after being inserted into the target number, as shown in the following figure:

This function looks very simple, but you may not know it, it also has important uses in distributed systems.
Suppose now you have 10 single nodes of Redis for distributed caching. For some reason, you can’t do clustering. When you want to search for a piece of data, you must first make sure that the data is in Redis. If it is, read the data directly from Redis; if not, read it in the database first, and then cache it in Redis.
Because of the large amount of data, you cannot store the same data in 10 Redis nodes at the same time, so you need to design an algorithm to store different data in different Redis nodes.
When you want to query data, you can query which Redis the data (if in the cache) should be stored in according to this algorithm.
Students with a little experience in distributed system design will definitely think that this is simple, 10 Redis nodes number 0-9. Calculate the hash value for the key , this hash value is a 32-bit hexadecimal number, which can be converted into After decimal, find the remainder of 10, and what the remainder is, put it in the corresponding node.
In this way, as long as a new data comes, you only need to go to the Redis corresponding to the remainder to determine whether it has a cache or not.
But here comes the problem. If you start to use this method and there is already data in Redis, the number of your Redis nodes cannot be changed. Once you add or subtract 1 node, all the remainders are changed, and the Redis node found by the new data must be wrong. For example, the hash value of the key was originally divided by 10, and the remainder was 2. Now it is divided by 9, and the remainder is 1. You should have gone to Redis No. 2 to find the cache, but now you go to Redis No. 1 to find the cache, you must not find it.
How to solve this problem? Let’s demonstrate with a simple example. Suppose I now have a list: [200, 250, 300, 400, 500, 530, 600] . Each number represents a house at that price point. The unit is ten thousand. You want to buy a house, but the cheap house is too shabby and the good house is too expensive. So you only look for houses with a price equal to your expectations, or slightly higher than your expectations but with the smallest gap.
Suppose now your expectation is 2.5 million, and a house happens to sell for 2.5 million, so you can buy it.
Suppose now your expectation is 4.7 million, then your only option is a 5 million house.
It should be pretty well understood by now, so let’s add or subtract candidates:
- The 5 million house was bought by someone else. The list becomes
[200, 250, 300, 400, 530, 600], so the only thing that works for you is a house of 5.3 million. - If the 2.5 million house is now bought, the list becomes
[200, 300, 400, 500, 530, 600]. At this time, it has no effect on you, and the house suitable for you is still a 5 million house. - If now a 4.8 million house is added, the list becomes
[200, 250, 300, 400, 480, 500, 530, 600]. Then the right house for you now becomes 4.8 million. - If a 2.4 million house is now added, the list becomes
[200, 240, 250, 300, 400, 500, 530, 600]. At this time, it has no effect on you, and the house that is suitable for you is still 5 million.
In this scenario, we can just use bisect.bisect_left() ! Results as shown below:
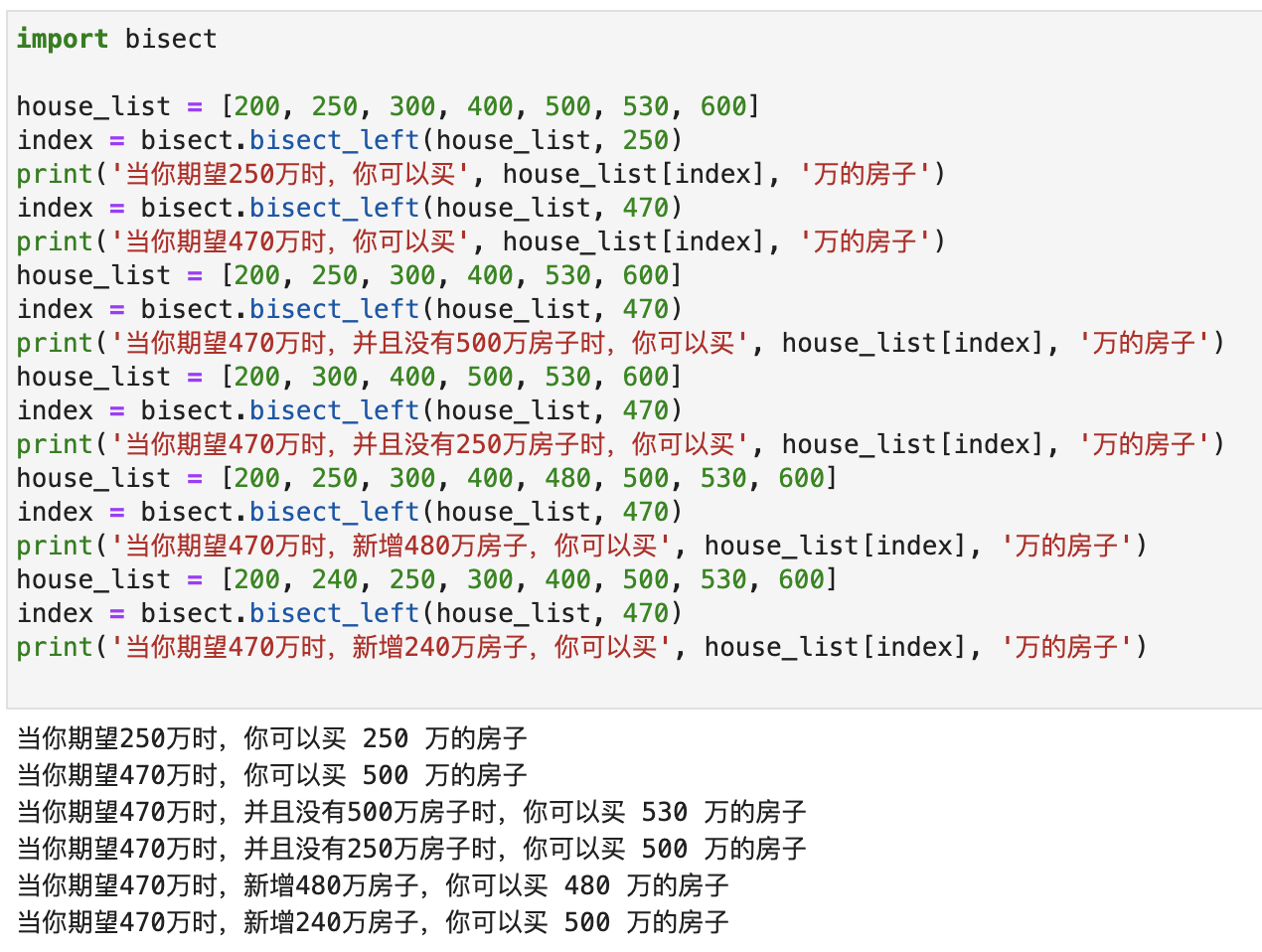
When an alternate option is changed, only the houses near your target option are affected. Changes in houses smaller than your candidate and more expensive houses will have no effect on you.
Did you notice that this scenario is very similar to our distributed cache adding and removing Redis nodes. We used to have 10 Redis, and now we have added one and it has become 11. Then only part of the cache of one Redis will be migrated to this newly added Redis. The other 9 Redis caches do not need to be changed.
Similarly, when we delete a Redis node, the data in the deleted node only needs to be synchronized to another Redis node next to it. The other 8 Redis nodes do not need any modifications! (It can also be out of sync. Only a small number of keys will not find the data due to deleting this node, and the database will be re-read. 80% of the cache will not be affected in any way.)
This is the consistent Hash algorithm.
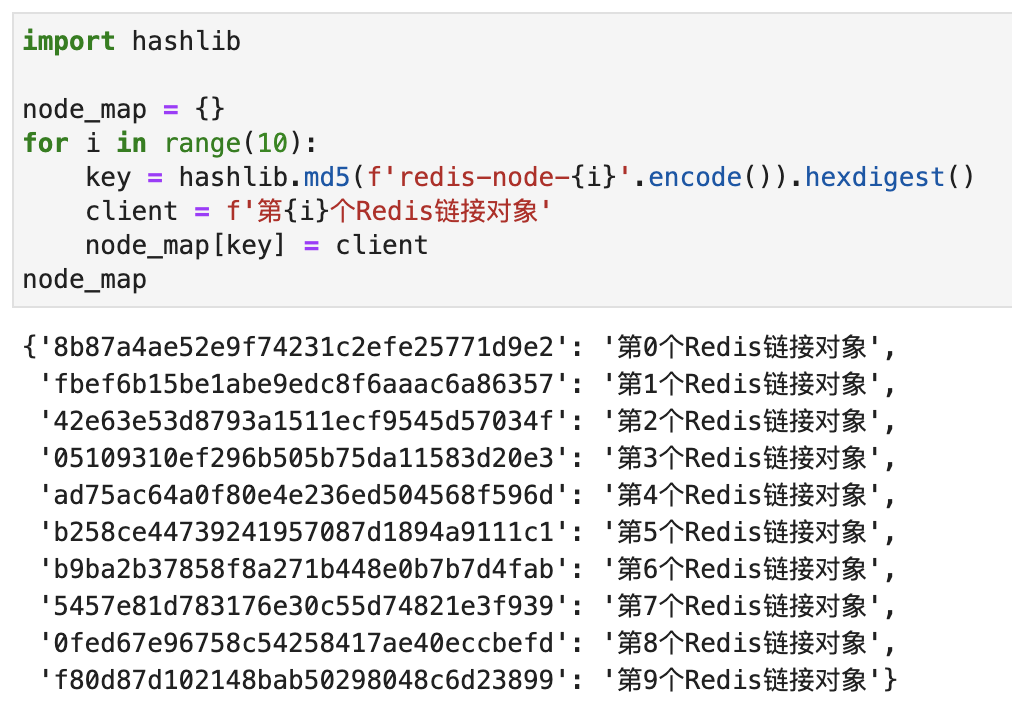
Let me briefly describe the implementation of this algorithm. First, we create 10 connection objects using redis.Redis(不同redis的连接参数) . Then create a map with each connection object and a Hash value, as shown in the following figure:
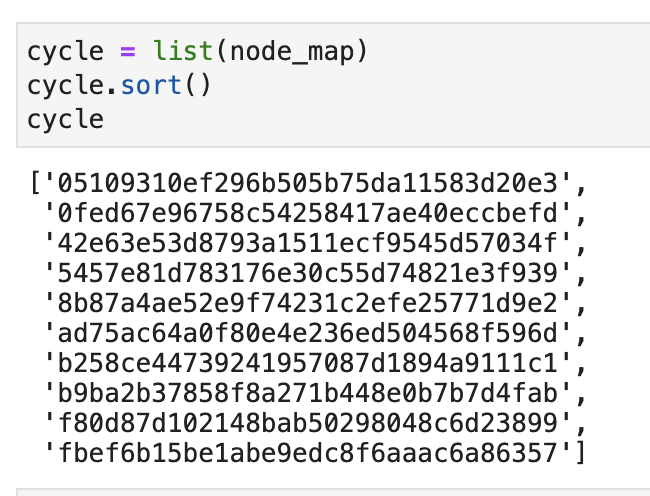
Then, we sort these 10 hash values and put them into a list. As shown below:
Now, there is a new cache query request, we calculate the hash value corresponding to the key, and then use bisect.bisect_left() to find the index of the hash value of the corresponding Redis node in the list. If the returned index is equal to the length of the list, then let the index equal to 0. After finding the index, get the Hash of the corresponding Redis node, and finally use this Hash to find the corresponding Redis node. The simplified code is as follows:
`
If you add or delete Redis nodes, you only need to update node_map and cycle . Only a small data migration occurs, and it does not affect the vast majority of caches. For example, I now delete the Hash corresponding to the第1个Redis链接对象: fbef6b15be1abe9edc8f6aaac6a86357 from node_map and cycle . If you query again, you will find that the Redis node numbered 6 is still found.

Consistent Hash is widely used in distributed systems. But you may not think that its core principle is bisect_left in binary search.
Of course, the above is just a simplified algorithm. The complete algorithm of consistent hash also involves virtual nodes and algorithms to avoid data skew. If you are interested, I can also write an article to fully explain its algorithm implementation.
This article is reprinted from: https://www.kingname.info/2022/06/22/bisect-left/
This site is for inclusion only, and the copyright belongs to the original author.