Original link: https://blog.chungzh.cn/articles/binary-indexed-tree/
I have learned the line segment tree for a long time, but I am ashamed that the simpler tree-like array has not been deeply understood, and it only stays at the level of memorizing the code. Learn about tree arrays seriously today.
introduce
Tree arrays (Binary Index Tree, BIT / Fenwick Tree) support two simple operations, single-point modification and interval query , and the time complexity is $O(\log n)$. Its implementation is simpler and faster than segment trees, but slightly less powerful.
principle
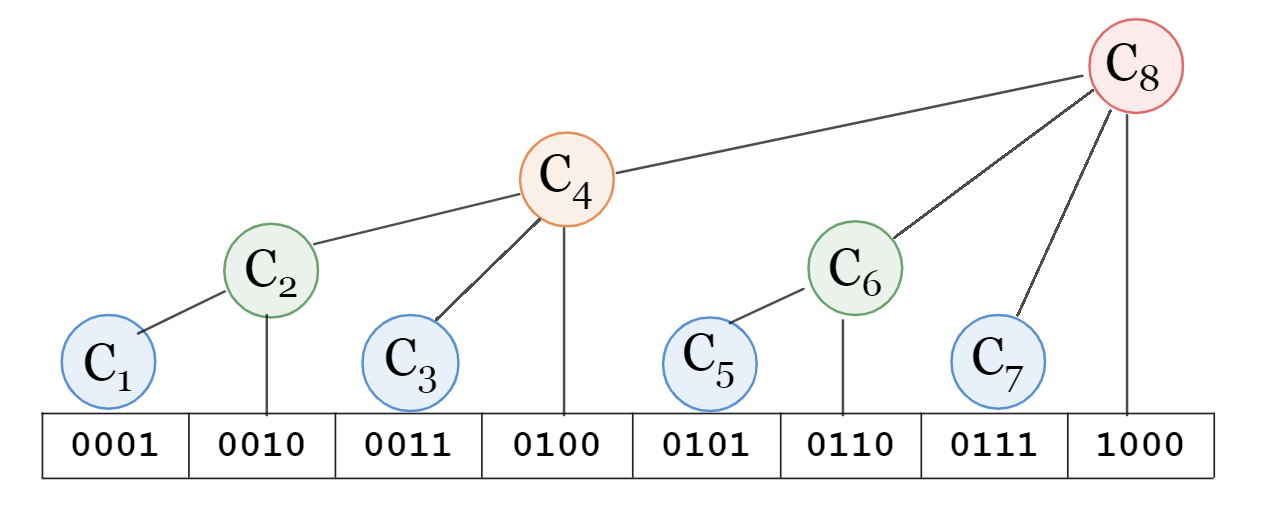
We use $C_i$ to represent a section of the $A$ array, define the binary representation of $x$, the position of the lowest $1$ is $\operatorname{lowbit}(x)$, then use $C_i$ to represent $ The subscript range $[i-\operatorname{lowbit}(i)+1, i]$ of the A$ array. For example, $4_{(10)} = 100_{(2)}$, $100_{(2)}-\operatorname{lowbit}(100_{(2)})+1_{(2)}=1_ {(2)}=1_{(10)}$, then the interval represented by $C_4$ is $[1, 4]$. Through this design, the tree-like array compresses the number of nodes to the same length as the array, unlike the line segment tree that requires $2n$ nodes.
The reason for this feature is that for the position $i$, the height of the corresponding node is the number of bits of $\operatorname{lowbit}(i)$. The first-level nodes are all $2^0 + 2^1k$, that is, all numbers of $\operatorname{lowbit}(i)=1$; the second-level nodes are all $2^1 + 2^2k$, that is All numbers of $\operatorname{lowbit}(i)=2$; the third level node is all $2^2 + 2^3k$ , that is, all numbers of $\operatorname{lowbit}(i)=4$; And so on. That is to say, for the position $i$, trace vertically upwards at this position, and the number of layers that can be traced is the number of $0$ at the end of the binary representation of $i$. The height of the node determines the size of its subtree, so the size of the information interval it represents must be $2^{the number of 0s at the end of i}=\operatorname{lowbit}(i)$.
*From Reference 1
accomplish
How is $\operatorname{lowbit}$ calculated? We have this formula: $\operatorname{lowbit}(x)=(x)&(-x)$. In computers, signed numbers are represented in two’s complement. In two’s complement notation, the opposite of $x$ -x = ~x + 1 , that is, the bitwise negation plus one. For example, the location of the last $1$ of $x$ is $\cdots 01000\cdots$, after the bitwise negation is $\cdots 10111\cdots$, and it is added again and again to become $\cdots 11000\cdots$; The bits are the opposite of the original. At this point, we do bitwise AND with $x$, and the result is $01000\cdots$, which is $\operatorname{lowbit}(x)$.
single point modification
The modification operation is similar to the process of climbing up a tree. For example, if we want to modify the third element, then we need to modify $C_3, C_4, C_8$ in turn, which is $11, 100, 1000$ in binary, and find that the subscript $x$ needs $x += \operatorname{lowbit every time }(x)$ until the top is reached.
|
|
Interval query (prefix sum)
For example, query the prefix sum of the sixth element, that is, the interval $[1, 6]$. First, the interval represented by $C_6$ is $[5, 6]$, and then jump to $C_4$, which represents the interval $[1, 4]$, and it is OK to add up. How did you jump from $C_6$ to $C_4$? It’s actually $110 – \operatorname{lowbit}(110) = 100$. So the subscript $x$ requires $x -= \operatorname{lowbit}(x)$ every time until $x<1$.
|
|
As for the sum of the interval $[a, b]$, you only need to find $[1, b]$ and $[1, a)$ respectively and then subtract them.
$O(n)$ build tree
The brute force method is to make $n$ single-point modifications, and the time complexity is $O(n\log n)$.
There are two ways to achieve $O(n)$ tree building.
prefix sum
As mentioned earlier, the interval represented by $C_i$ is $[i-\operatorname{lowbit}(i)+1, i]$, then we can preprocess a $sum$ prefix and array first, and then calculate the $C$ array.
|
|
Contribute backwards
We can easily know that the father of the current point $i$ is $i+\operatorname{lowbit}(i)$, so update the father with its own value.
|
|
References
- What is the principle of tree array? – SleepyBag’s answer – Knowing
- Algorithm Study Notes (2): Tree Array – Pecco’s Article – Knowing
This article is reproduced from: https://blog.chungzh.cn/articles/binary-indexed-tree/
This site is for inclusion only, and the copyright belongs to the original author.