Introduction: When I read Raft’s big paper before, I didn’t understand the part of “cluster change”. So I recently re-read this part of the big thesis, and the following are some records I made during the re-reading. This part of the content is planned to be divided into two articles. This is the first article, which mainly explains the theoretical basis of the member change process, and the second article explains the problems in practice.
Rereading the Cluster Membership Change Algorithm in Raft Papers (1): Theoretical
“Cluster membership change” refers to the addition and deletion of nodes in a cluster, which is an essential operation in a distributed system because there is no guarantee that all nodes in a cluster can always work very good. Raft’s big paper ” Consensus: Bridging Theory and Practice ” has a dedicated section to explain this part.
safety
First of all, the Raft algorithm requires all operations to ensure safety, that is, there can be no two leader nodes in the cluster at the same time. The “cluster member change” algorithm must also ensure that the major premise of security cannot be violated, so the paper explains why it is not allowed to directly change multiple nodes:

In the illustration above:
- The old cluster has three nodes, 1, 2, and 3, and it is necessary to change the new nodes 4 and 5 of the three-node cluster to a 5-node cluster.
- If you change it directly as shown in the figure, because the time window of each node is not consistent, this may happen:
- At a certain point, nodes 1 and 2 are still using the member configuration of the old cluster (containing only {1,2,3}), while 3, 4, and 5 are already new clusters (containing {1,2,3,4) ,5}) members are configured.
- In this way, it is possible that a leader is elected by 1 and 2 that also use the old cluster node configuration, and another leader is elected by nodes 3, 4, and 5 that have already used the new cluster configuration, thus violating the above-mentioned “” security” requirements.
It should be noted that in the above example of the error, the error is caused by the simultaneous occurrence of two types of behaviors:
- Change multiple nodes at once. In the example, 4 and 5 nodes are added to the cluster at one time.
- Change directly. The direct change is because the steps of different nodes in the cluster are different, and if two different clusters appear on different nodes, it may lead to the selection of two different leaders.
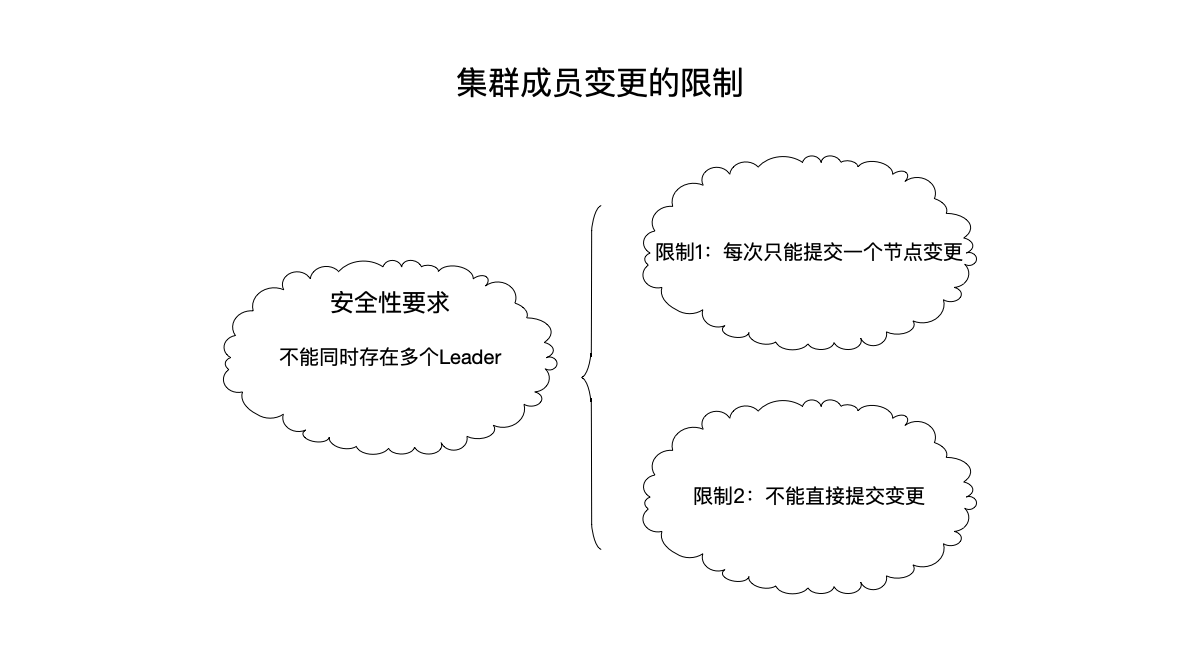
Therefore, since these two error operations occur together to cause errors, two solutions are given in the paper:
- Or strictly limit changes to only one node at a time.
- If you really want to change multiple nodes at one time, you cannot change them directly. You need to go through an intermediate state transition before you can complete the operation of changing multiple nodes at the same time.
The two different implementations are described below.
Change a single node at a time
If it is limited to change only one node at a time, then it can be ensured that “the quorum sets of the new and old sets are overlapped.” security can be indirectly guaranteed.
The paper uses the following examples to illustrate the correctness of this operation:
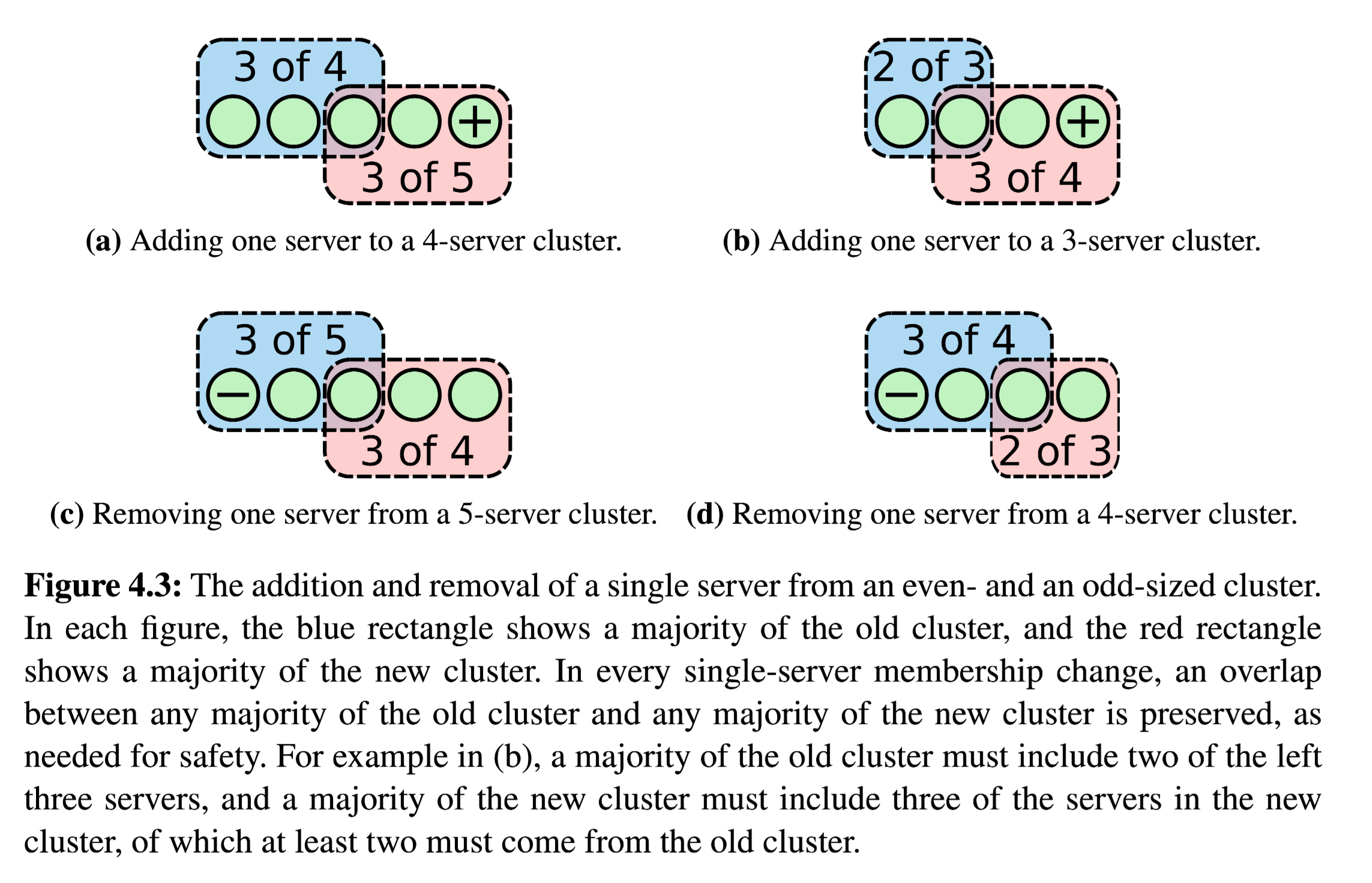
These figures are demonstrated in two dimensions:
- Add and delete operations.
- Whether the number of original cluster nodes is odd or even.
The combination of the two dimensions is the same as the above 4 cases, but in either case, since the condition of “the quorum sets of the new and old sets are overlapped” is guaranteed, so different leaders will not be selected to come .
Change multiple nodes at once
As can be seen from the above example: as long as it is guaranteed that only one node is changed at a time, it can be changed directly. That is: without an intermediate state, directly change from set A to set A+1, because the quorums of these two sets must overlap.
However, in the case where multiple nodes need to be changed at one time, it cannot be directly changed in this way, because two leaders will be elected at the same time as in the first example. Therefore, in order to solve this problem, an intermediate state needs to be introduced:
- Assuming that the original cluster node set is C_Old and the new cluster node set is C_New, then first change the configuration to {C_Old, C_New}, which is the union of the old and new cluster node sets.
- After the above change is submitted, change the configuration to C_New to the cluster. After this change is submitted, those nodes that are not in the C_New node set will automatically go offline and exit the cluster when they receive this change.
It can be proved that in the above two steps, there will be no situation of “two leaders exist at the same time”.
In essence, this change algorithm belongs to a two-stage member change algorithm, which is called the “Joint Consensus” algorithm in the Raft paper. The following figure demonstrates the flow of these two stages of the Joint Consensus algorithm:
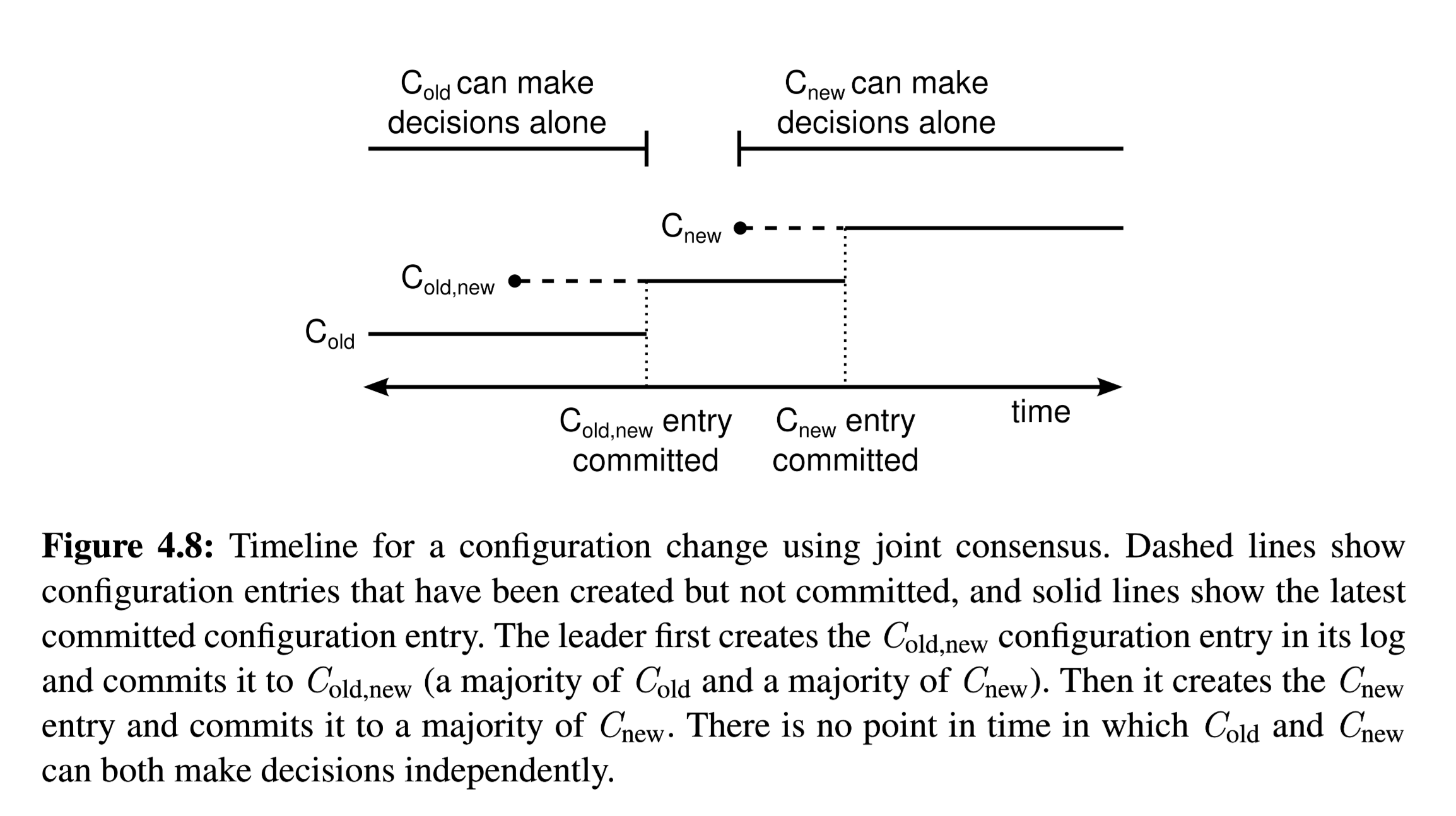
Failover
Let’s take a look at the Joint Consensus algorithm. If an error occurs during the change process, how failover selects a new leader.
In the first stage, there are only two possible cases for the candidate leader, either the old C_Old node set, or the {C_Old, C_New} node set that has been received:
- Nodes with only C_Old node set: Since this leader does not have the {C_Old, C_New} node set changes submitted in the first stage at this time, the logs of the followers who already have {C_Old, C_New} node sets will be truncated, and members will be truncated. If the change fails, fall back to the C_Old collection.
- A node with {C_Old,C_New} node set: This means that the leader has already changed the {C_Old,C_New} node set submitted in the first stage, and can continue to complete the unfinished member change process.
Similarly, it can also be deduced that when the leader is down in the second stage, the elected leader may only have two situations, but it is impossible to elect multiple leaders in both situations.
When do cluster changes take effect?
After explaining the two different cluster changes, let’s talk about when the cluster changes take effect.
In the consensus algorithm of state machine models such as Raft and Paxos, any change operation is regarded as a command (Command). The command processing flow is as follows:
- When the state machine receives a command, it first persists the command locally.
- Then broadcast to other nodes in the cluster.
- When a response is received from more than half of the nodes in the cluster, it is considered that the command can be submitted (commit), so it can take effect and pass the submitted logs to the state machine of the application layer for use.
The above process can be seen: a command can only “apply” after “commit”.
In Raft, the operation “member change” is also a type of command, namely:
struct Command { LogEntry, MembershipChange, };
The advantage of this design is that the processing of member change operations is no different from the general log, so there is no specific time called “processing member change time”, during which time it stops responding to general commands.
But unlike general orders, the “member change” operation does not need to wait for a majority to take effect. Note that for general commands, to “validate”, you must first “commit”, and cluster change commands do not have this dependency.
That is, in the member change process of Raft, after the node receives a new cluster node configuration, it will take effect immediately, and there is no need to wait for more than half of them to pass.
This is an often overlooked part of reading this part of the Raft paper. Why does the cluster change class command, can it do this, and will it be a problem to do so?
For security, when Raft performs a cluster change operation, whether it is “changing one node at a time” or “changing multiple nodes at a time”, there can be no overlap in different stages, because overlapping means that May violate the security mentioned earlier. For example, to change a cluster node set from {1,2,3} to {1,4,5}, if you use these two methods, the steps are:
- Change one node at a time: {1,2,3}->{1,2,3,4} (add node 4)->{1,2,3,4,5} (add node 5)->{ 1,3,4,5} (remove node 2) -> {1,4,5} (remove node 3).
- Change multiple nodes at once: {1,2,3}(C_Old)->{1,2,3,4,5}({C_Old,C_New})->{1,4,5}(C_Old, C_New).
As you can see, either way, there are multiple steps. The leader decides the current step, and its judgment standard is: whether the log modified in the previous step has been submitted (more than half agree). Therefore, if the log of the member change class takes effect after submission, the leader needs one more step:
- First, confirm that the log has been submitted to more than half of the nodes.
- After this, confirm that the member change has taken effect on the node.
The latter confirmation can be avoided. Because according to the analysis of the previous failover section, no matter which situation occurs, even if the leader goes down during the change process, there will be no situation where multiple leaders are selected.
Therefore, for the log of member change classes, Raft’s rules are:
- Multiple commits cannot overlap (overlap), that is, if there is already an uncommitted member change log, it is not allowed to commit new member changes before it is committed.
- The member change takes effect without waiting for submission. When each node receives such a log, it can immediately modify the member on the node to the latest configuration.
Summarize
- The Raft algorithm requires safety at all times: there cannot be two different leaders in the cluster at the same time.
- A security breach is possible if both of the following actions occur at the same time:
- Change multiple nodes at once.
- Directly alter the node set of the cluster.
- Starting from these two constraints, there are the following two algorithms for implementing member changes:
- Only one node can be changed at a time. In this case, members can be changed directly.
- Any number of nodes can be changed at a time, but it must be completed through a two-phase commit to take effect: the first time from C_Old to {C_Old, C_New} node set, the second time from {C_Old, C_New} to C_New.
- The “member change” class command is also a log in the Raft algorithm. However, unlike ordinary log commands, the member change log can take effect without waiting for the log to be submitted, and it can take effect immediately after it is received.
This article is reprinted from: https://www.codedump.info/post/20220417-weekly-13/
This site is for inclusion only, and the copyright belongs to the original author.